Anonymisation and pseudonymisation (II): Differential privacy
The strategic value of personal data for companies and organisations is obvious. However, the risk that the massive processing of personal data poses to the rights and freedoms of individuals and to our model of society is equally undeniable. For this reason, it is necessary to adopt the necessary guarantees so that the processing carried out by the different data controllers does not entail an interference with the privacy of individuals. In the search for a balance between the legitimate exploitation of information and the respect for individual rights, strategies aimed at preserving the usefulness of data while respecting their privacy are emerging. One of these strategies is differential privacy.

The US Census Bureau, in order to ensure the accuracy of its statistics, prevent personal information from being revealed through its statistics, and thus increase citizens' trust in the security of the data they provide, is applying differential privacy.
Differential privacy can be categorised as one of the privacy enhancing techniques (PETs) aimed at establishing data protection guarantees by design through the practical implementation of information abstraction strategies. As described by its creator, Cynthia Dwork, differential privacy guarantees, despite the incorporation of random noise into the original information, that the result of the analysis process of the data to which this technique has been applied does not suffer losses in the usefulness of the results obtained. It is based on the Law of Large Numbers, a statistical principle that states that when the sample size grows, the average values derived from it approach the real mean value of the information. Thus, the addition of random noise to all the data compensates for these effects and produces an "essentially equivalent" value.
The concept "essentially equivalent" does not mean that the result obtained is identical, but refers to the fact that the actual result from the analysis derived from the original data set and the result from the set to which differential privacy has been applied are functionally equivalent. This circumstance allows for the "plausible deniability" of a particular subject's data being in the dataset under analysis. For this purpose, the noise pattern embedded in the data has to be adapted to the processing and the accuracy margins that need to be obtained.
At first sight, the behaviour described above allows two important conclusions to be drawn:
- This strategy seeks to protect the results of the analysis of the information, which is what is to be disseminated. Therefore, it does not alter the original data, but acts on the transformation process or algorithm for querying and publishing the analysed data.
- As a consequence, and unlike other privacy assurance techniques, it does not require a detailed analysis of other possible data sources that could be used to establish relations with the input data or of the possible attack models used. With this technique, the focus of the information privacy enhancement strategy is on the data analysis process employed and not on the characteristics of the data as such.
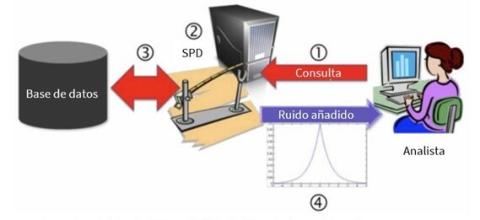
1. The data analyst launches the query to the software that implements differential privacy (SPD).
2. The SPD assesses the privacy impact of this query on the data.
3. The SPD redirects the query to the database and obtains the actual and complete response to the query.
4. The SPD adds the amount of noise necessary to distort the query result according to the privacy budget
and sends the modified response back to the data analyst.
Image taken from Microsoft's note "Differential Privacy for Everyone"
More specifically, differential privacy relies on the use of mathematical functions (also called mechanisms) that add random noise to the results of the query performed. In this way, it is possible to specify the confidence level of the results based on the parameter ɛ or privacy budget, which establishes the balance between the precision of the query result (accuracy) and the protection of the queried information (privacy). In other words, the built-in noise masks the difference between the real analysis scenario, which would include all the records, and the exclusion scenario in which the records associated with the subject have been eliminated from the overall set of data, so that the result obtained differs only in the built-in noise (and which is set by the value of ɛ).
The great advantage of this technique is that the loss of privacy, as well as the accuracy of the analysis, can be objectively quantified, as well as the privacy risk accumulated as a consequence of successive queries on the same dataset. Mathematically expressed, the analysis is performed by considering two databases: BD1, the complete set of data, and BD2, the set of data excluding one record. The ratio of the probability of obtaining a result R when applying a query mechanism Ŋ on BD1 over applying Ŋ on BD2 and obtaining the same result is expressed as:
Pr [Ŋ (BD1) = R] / Pr [Ŋ (BD2) = R] < e ɛ
In the particular case that ɛ=0 we will have absolute privacy as a consequence of the very definition of differential privacy: if ɛ=0, Pr [Ŋ (BD1) = R] = Pr [Ŋ (BD2) = R], so that the mechanism Ŋ will be totally independent of the subset of analysis data selected. If ɛ is non-zero, but with a value small enough to approximate the ratio to 1, then we have a differential privacy scenario.
The obvious question is how to objectively calculate the value of noise that needs to be added to obtain a value of ɛ that preserves the result within the utility range.
To do this, it is necessary to take into account another concept which is that of overall sensitivity, which can be obtained by measuring the specific weight of a record on the result of the query. In the case of numerical values, it is the maximum difference between two adjacent data sets (i.e. those that differ in only one of the records). The value of the noise added by the mechanism Ŋ is conditioned by the overall sensitivity and can be expressed as:
Δ Ŋ = max [Ŋ (BD1) - Ŋ (BD2)]
In general, differential privacy works best with those types of analysis with low overall sensitivity, as long as, by adding noise, it is possible to maintain data privacy without distorting the value of the actual query result above the utility threshold.
There are different types of analysis to which differential privacy can be applied: occurrence counting, histograms, linear regressions, cumulative distribution functions, machine learning, etc., used in practical applications beyond those already known from Google, Apple or Microsoft, such as, for example, Uber in the analysis of the distance of journeys. Another practical example of the use of differential privacy is the monitoring of heart rate data collected through a wearable. The smart device identifies prominent points in the data streams and then, by applying local differential privacy, perturbs them by adding noise before sending them to the server for reconstruction, analysis and storage.
More information on privacy engineering and other techniques used in data protection by design can be found on the Innovation and Technology website of this Agency, as well as on our blog:
10 Misunderstandings related to anonymisation
Introduction to the Hash Function as a Personal Data Pseudonymisation Technique
K-anonymity as a privacy measure


